Quantum surgery: the quantum mechanics insight beyond the uniportal video-assisted thoracic surgery (VATS) approach
Introduction
The progressive refinements of the uniportal video-assisted thoracic surgery (VATS) were associated with a wider variety of surgical reasons, including extensive anatomic pulmonary resections for lung malignancies (1). Literature has previously established the advantages of uniportal VATS over standard multiport procedures in postoperative pain reduction, shorter hospital stays, and quicker return to normal activities (2). Suppose the ergonomic and geometrical aspects of uniportal VATS in Euclidean geometry have already been investigated (3-5). In that case, nothing has been said about the technique’s potential non-Euclidean geometric and quantum characteristics. We discuss the possible quantum mechanics insights in the uniportal VATS approach.
A brief reminder on geometrical aspects of uniportal VATS
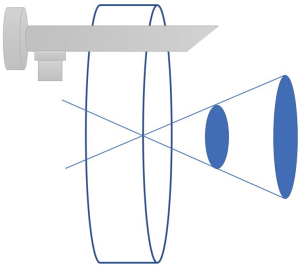
In earlier articles, the geometric features of uniportal VATS were described: one tiny incision without additional dissection of the intercostal region, with the simultaneous entrance of tools and the thoracoscope through a perfect circular truncated cone as broad as a surgeon’s fingertip. Simple zooming in/out of the operating field enables the thoracoscope to display the position of the instruments during the process. In uniportal VATS, enhanced hand-eye coordination is also necessary to visualise and control the thoracoscope-instruments ensemble. They should be crossed at the port’s entrance to form a triangulation with mostly curved surgical tools (Figure 1). The crossed tools provide a more excellent range of motion, but the subsequent reversal of handedness poses major mental adaptation issues for the surgeons (3-5).
Quantum mechanics features of mental adaptation
In examining the surgeon as a whole, one comes up immediately with the issue of mental adaptation and how it fits a physical existence. Plato first described that memory is stored in the brain through physical alterations (6). Up-to-date neurophysiology examines how the brain, through synapse plasticity, is related to memory and learning. Moreover, modern quantum mechanics has played a significant role in mental adaptation. Many founders of quantum mechanics regard this theory more as a guidepost of how the mind interacts with the environment (7). Quantum mechanics is the magic of entanglement crucial for life, which implies that it is critical to understanding the surgeon’s mental adaptation. The success of quantum mechanics is due to the close correspondence between its theoretical computations and experimental observations. To capitalise on such accomplishments, neurosciences must embrace the formalism required to comprehend quantum events at the cell level, which is a prerequisite for understanding the tremendous computing capability of the brain (8). Numerous eminent physicists, including Niels Bohr, Max Planck, Werner Heisenberg, Wolfgang Pauli, and Erwin Schrodinger, deemed observations and measurements important. The classic von Neumann interpretation of conventional quantum theory holds that the quantum state of a quantum system evolves deterministically in unitary time.
Nonetheless, measurement interrupts this development, and a specific value of the system emerges, as predicted by quantum probability theory. Quantum theory cannot predict which exact value will arise in any case. Observational decisions in the laboratory shape the context of what is to be observed, and according to Richard Feynman, quantum systems have no attributes without observation (7).
Quantum philosophy uniportal VATS
The rigid instruments passing the incision of uniportal VATS are only maneuverable like an oar of a rowing boat since the incision, as a fulcrum, limits the device’s movements to 4 degrees of freedom (Figure 2). This impact makes it difficult for the surgeon to move or reach tissues from multiple directions without further incisions. Using curved or articulated devices might allow for several approaches to a specific region without needing an additional incision. The curved design permits tissue manipulation by moving the shaft and turning the tip toward the target. Nevertheless, the tip motion is constrained by the degree of instrument curvature. The usual operation of uniportal VATS necessitated using two instruments with different angulations.
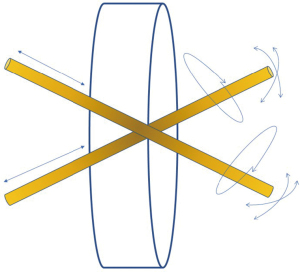
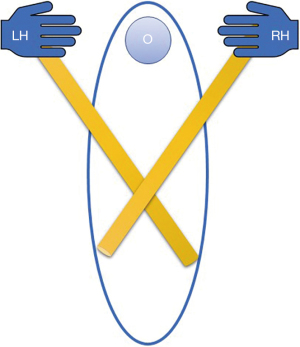
Consequently, the motion of a curve is often conveyed by rotating the entire shaft. In this manner, the tip and the curved portion will rotate, resulting in an unintended hooking action that might result in accidents with other instruments. According to prior laparoscopic research, four fundamental manipulation strategies exist for the devices utilised in uniportal VATS. The drawbacks of the internal crossing manipulation (Figure 3) include external hand collisions and the complexity of manipulating the tooltips. Utilising curved gadgets, a crosshanded method should be devised. For the safe dissection of target tissues, the surgeon’s left hand must operate the tools on the right and vice versa to prevent internal instrument conflict. These motions create a complete degree of freedom in the fulcrum of the uniportal access; hence, there are no instrument conflicts, and a safe approach to the target tissue may be made (3).
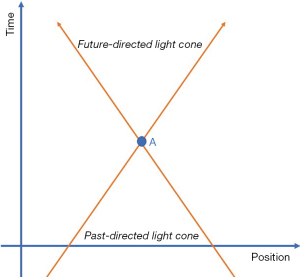
In this configuration, a Minkowski space could be recognised. If event A is in the past-directed cone of event F, it would be possible for event A to affect the event in the cone. However, since event C is outside the cone, it cannot affect event A. Likewise, A can influence D if event D is in the future-directed light cone (Figure 4). If we transfer what has been explained before to the “surgical act”, here is that the surgeon, who is thinking the action that is going to be performed, is the event A, in the past-directed cone of the event F (the movement of surgical instruments he makes for reaching the target). Event D is the final surgical act made on a patient in the future-directed cone, which had to be thought in the surgeon’s mind a while before being performed. Mathematically and by relativity, space and time are interchangeable.
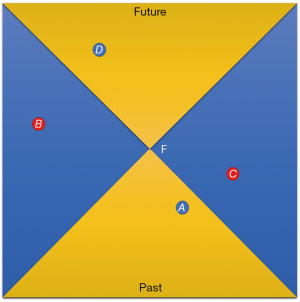
However, we know they form co-equal parts of a significant space-time. It is only within space-time that physicists can rigorously understand the complete understanding of the motion and properties of natural objects and phenomena. Space and time are to space-time what arms and legs are to individuals. They are substitutable, but it is impossible to comprehend 10,000 years of history without including arms and legs as part of the essential anthropological condition. The Polish mathematician Hermann Minkowski elegantly described special relativity due to the makeup and mixture of space and time. Minkowski preserved space and time as two interlinked parts of the same whole. In the Minkowski space, each event has a position in space and a position in time. In Minkowski’s space, objects exist and move between places. The line representing the path through space and time is named worldline. If an object is motionless, the world line is vertical.
On the contrary, if an object is moving, the worldline is at an angle, and the slope is a function of the object’s speed. Because nothing can travel faster than light, the light cones determine what events in the past can affect current events and what events in the future can be affected by the present (Figure 5). As the time and space axes move together, all non-light-like events are smashed together by the axes (9).
If it can be true for any surgery, it is even more true for uniportal VATS. Indeed, while in other surgeries, there is an entirely immediate and automatic head-hand-target consequentiality, in uniportal VATS, in the beginning, the surgeon (A) has to think—a few seconds before—about how to make the crossing manipulation (F) in order to perform the surgical act (D) without instrument fencing and to achieve an automatism. Again, as in any quantum system, any event can happen in F until it is observed and measured. Moreover, in the flow of movements during surgical manipulation of instruments, event F occurs as a precise and efficient gesture when observer C measures it. The event F appears because observed.
Simply put, the observer (C) cannot interfere with the surgical gesture. However, he has the power to record the act, observe it at that moment, measuring and evaluate it. If we want, this is the “quantum reading” of the underlying learning process in uniportal VATS, based on careful observation of expert uniportal surgeons operating during masterclasses or live operations.
Projective geometry accurately depicts the imaging process of VATS because it permits a far more important class of transformations than only translations and rotations, namely perspective projections. To comprehend why knowledge of projective geometry is essential to grasp the optical advantages of uniportal VATS, we must begin with Euclidean geometry. In two-dimensional geometry, two lines nearly invariably intersect at a point. Parallel lines meet at infinity, extending the Euclidean plane by adding these points at infinity where parallel lines meet. This solves the problem with infinity by referring to them as ideal points. By adding these points at infinity, the conventional Euclidean space becomes the projective space, a new sort of geometric object. Projective space is an extension of Euclidean space in which two lines always intersect at infinity at a single point. It turns out that the point at infinity in two-dimensional projective space forms a line commonly referred to as the line at infinity. In the three-dimensional view, they form the infinite plane. There are no points at infinity in the real world, such as the line at infinity in the flat picture and the plane at infinity in the globe.
Even though we often work with projective spaces, we recognise that the line and plane at infinity are unique. We also attempt to have our cake and eat it by considering all points in projective space as equal when convenient and singling out the line at infinity in space or the plane at infinity in the picture when it becomes required. The uniportal technique demands the movement of the thoracoscope instruments at 90° along a sagittal plane, therefore allowing the instruments to approach the target lesion from a vertical caudo-cranial vantage point (4).
Henceforth, the popular conception of time as the river of time, based in part on Isaac Newton’s statement in the principia that time flows equably without relation to anything external, as well as Minkowski’s promotion of time as a fourth dimension, may need to be revised to a description of a rotational entity. Therefore, adopting a water analogy, time would be described as a swirling river (9,10). The human intellect is excellent yet limited, and we cannot comprehend certain things. The dimensions of the cosmos have always been and will continue to exist solely in human imaginations. We inhabit a universe where Newtonian mechanics reign supreme and Einsteinian-relativistic physics is irrelevant. If the vastness of the universe is incomprehensible to us, the peculiarities of the incomprehensibly little are much odd. Sir Richard Feynman stated that quantum theory was incomprehensible. This is significant, coming from a scientist of his status and ability. Our macroscopic reality is entirely alien to the weirdness and inconsistencies of quantum physics (the only world in which we exist and can know). In addition, certain quantum occurrences would be irrelevant to our universe. Theoretically, it may be feasible for most quantum particles in a book on a table to suddenly travel mainly in the same direction, causing the book to fly off the table. However, this never occurs in practice. However, his objective is difficult to attain, so this work has emphasised the topic (11).
Conclusions
Standard three-port VATS has a trapezoidal shape that interferes with the optical source by generating a new optical plane that causes an unfavourable torsion angle for standard two-dimensional displays. In contrast, the uniportal VATS approach to a lesion along a sagittal plane from a caudo-cranial perspective realises a projective plane that maintains intraoperative visual depth. The surgeon can bring the fulcrum into the chest by sliding the tools along parallel lines drawn from this plane. In this scenario, the uniportal VATS might provide quantum mechanics insights for a Minkowski space, and quantum surgery could become one of the last frontiers of surgical inquiry.
Acknowledgments
Funding: This work was partially supported by the Italian Ministry of Health with Ricerca Corrente and 5x1000 funds.
Footnote
Provenance and Peer Review: This article was a standard submission to the journal. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://shc.amegroups.com/article/view/10.21037/shc-22-30/coif). LB and LS serve as unpaid editorial board members of Shanghai Chest from August 2021 to July 2023. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Gonzalez-Rivas D, Paradela M, Fernandez R, et al. Uniportal video-assisted thoracoscopic lobectomy: two years of experience. Ann Thorac Surg 2013;95:426-32. [Crossref] [PubMed]
- Rocco R, Rocco G. Future study direction on single port (uniportal) VATS. J Thorac Dis 2016;8:S328-32. [Crossref] [PubMed]
- Bertolaccini L, Rocco G, Pardolesi A, et al. The Geometric and Ergonomic Appeal of Uniportal Video-Assisted Thoracic Surgery. Thorac Surg Clin 2017;27:331-8. [Crossref] [PubMed]
- Bertolaccini L, Rocco G, Viti A, et al. Geometrical characteristics of uniportal VATS. J Thorac Dis 2013;5:S214-6. [Crossref] [PubMed]
- Bertolaccini L, Viti A, Terzi A, et al. Geometric and ergonomic characteristics of the uniportal video-assisted thoracoscopic surgery (VATS) approach. Ann Cardiothorac Surg 2016;5:118-22. [Crossref] [PubMed]
- Plato: Theaetetus. Plato in Twelve Volumes. Cambridge, MA, USA: Harvard University Press, 1987.
- Kafatos MC, Yang KH. The quantum universe: philosophical foundations and oriental medicine. Integr Med Res 2016;5:237-43. [Crossref] [PubMed]
- Rocha AF, Massad E, Coutinho FA. Can the human brain do quantum computing? Med Hypotheses 2004;63:895-9. [Crossref] [PubMed]
- Chappell JM, Iqbal A, Iannella N, et al. Revisiting special relativity: a natural algebraic alternative to Minkowski spacetime. PLoS One 2012;7:e51756. [Crossref] [PubMed]
- Newton I. Philosophiae naturalis principia mathematica. Imprimatur S Pepys Reg Soc præses, 1686.
- Heffner DK. Infinitesimals, quantum mechanics, and exiguous carcinomas: how to possibly save a patient’s larynx. Ann Diagn Pathol 2003;7:187-94. [Crossref] [PubMed]
Cite this article as: Bertolaccini L, Nachira D, Margaritora S, Spaggiari L. Quantum surgery: the quantum mechanics insight beyond the uniportal video-assisted thoracic surgery (VATS) approach. Shanghai Chest 2023;7:10.